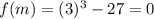Mathematics, 18.07.2019 04:10 foralways4871
Estimate the next guess for the root of x3 - 27 = 0 by using a modified bisection method as explained below. the initial bracket of (1.8,5.1) is found as a valid bracket. in the case of a modified bisection method, the root estimated at the end of the first iteration would be the point where the straight line drawn from the function at x = 1.8 to the function at x = 5.1 crosses the x-axis. what is this estimate of the root? (keep 4 decimal places)

Answers: 1
Another question on Mathematics

Mathematics, 22.06.2019 01:50
Order the equations from least to greatest based on the number of solutions to each equation.-4^x -1 = 3^(-x) – 2 -3x + 6 = 2^x+13^x – 3 = 2x - 2
Answers: 1

Mathematics, 22.06.2019 06:40
Match each function with the corresponding function formula when h(x) = 5 - 3x and g(x) = -3 x + 5. 1. k(x) = (3g + 5h)(x) 2. k(x) = (h - g)(x) 3. k(x) = (g + h)(x) 4. k(x) = (5g + 3h)(x) 5. k(x) = (3h - 5g)(x) 6. k(x) = (5h - 3g)(x)
Answers: 1


You know the right answer?
Estimate the next guess for the root of x3 - 27 = 0 by using a modified bisection method as explaine...
Questions

Mathematics, 21.10.2019 14:30

Chemistry, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30


Social Studies, 21.10.2019 14:30

History, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30

Geography, 21.10.2019 14:30

English, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30

Biology, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30

English, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30

Spanish, 21.10.2019 14:30

Chemistry, 21.10.2019 14:30

Mathematics, 21.10.2019 14:30


History, 21.10.2019 14:30

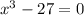 can be written as:
can be written as: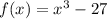 then:
then: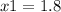 and
and 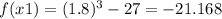
 and
and 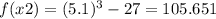
 which in our case is:
which in our case is: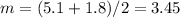 and
and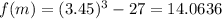
 and
and
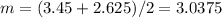 and
and 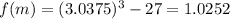
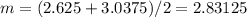 and
and 
 and
and 
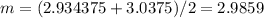 and
and 
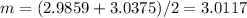 and
and 
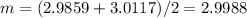 and
and 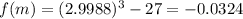
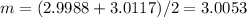 and
and 
 and
and 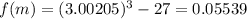
 and
and 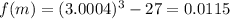
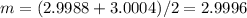 and
and 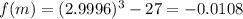
 and
and