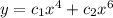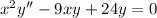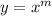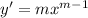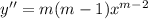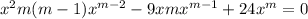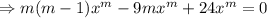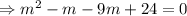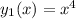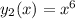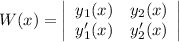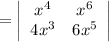Mathematics, 12.03.2020 02:30 emilymariec4036
Consider the differential equation x2y′′ − 9xy′ + 24y = 0; x4, x6, (0, [infinity]). Verify that the given functions form a fundamental set of solutions of the differential equation on the indicated interval. The functions satisfy the differential equation and are linearly independent since W(x4, x6) = ≠ 0 for 0 < x < [infinity]. Form the general solution. y =

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 21:30
Look at the figure below: triangle abc is a right triangle with angle abc equal to 90 degrees. the length of ac is 5 units and the length of ab is 4 units. d is a point above c. triangle adc is a right triangle with angle dac equal to 90 degrees and dc parallel to ab. what is the length, in units, of segment cd?
Answers: 1

Mathematics, 22.06.2019 00:00
Can someone me with this? i’m not sure what to put for my equations.
Answers: 2

Mathematics, 22.06.2019 02:40
The graph shows a vertical translation of y= square root of x cubedwhat is the range of the translated function? {yly < 0}{yly > 0}{yly is a natural number}{yly is a real number}
Answers: 3

Mathematics, 22.06.2019 04:30
Find the scale factor and ratio of perimeters for a pair of similar trapezoids with areas 49 cm squared and 36 cm squared.
Answers: 2
You know the right answer?
Consider the differential equation x2y′′ − 9xy′ + 24y = 0; x4, x6, (0, [infinity]). Verify that the...
Questions


History, 26.06.2019 03:30


History, 26.06.2019 03:30


Mathematics, 26.06.2019 03:30


History, 26.06.2019 03:30

Biology, 26.06.2019 03:30

Mathematics, 26.06.2019 03:30


History, 26.06.2019 03:30


Physics, 26.06.2019 03:30