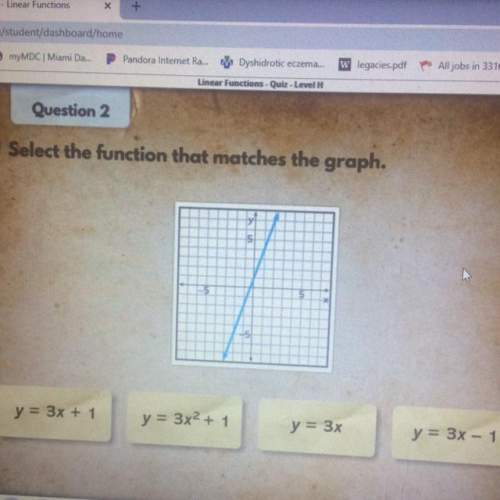
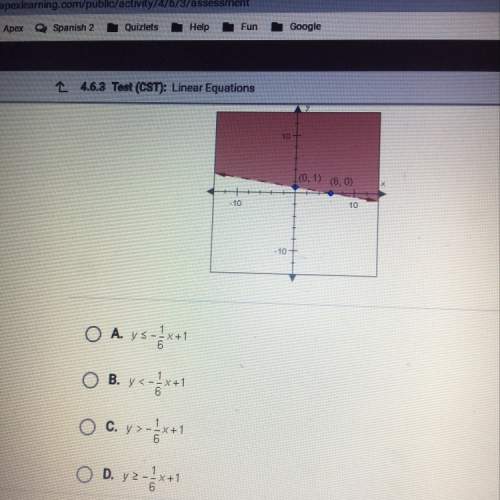
Mathematics, 21.04.2020 00:58 whitakers87
Let V be a vector space with subspaces Uand W. The set U∪W is the set of all vectors thatare in U or are in W. Give an example with V=R3 to show that U∪W need not be a subspace of V. In order to receive full credit, you must carefully explain how you know your example Uand W are subspaces of R3 and how you know U∪W is not a subspace of V.

Answers: 1
Another question on Mathematics


Mathematics, 21.06.2019 17:30
Suppose that an airline uses a seat width of 16.516.5 in. assume men have hip breadths that are normally distributed with a mean of 14.414.4 in. and a standard deviation of 0.90.9 in. complete parts (a) through (c) below. (a) find the probability that if an individual man is randomly selected, his hip breadth will be greater than 16.516.5 in. the probability is nothing. (round to four decimal places as needed.)
Answers: 3

Mathematics, 21.06.2019 18:30
The square pyramid has a volume of 441 cubic inches. what is the value of x? 1/7x is the height x is the base
Answers: 2

Mathematics, 21.06.2019 21:30
The expression 1.01*1.005(^t) gives the amount of money, in thousands of dollars, in carter's savings account (t) years after he opens it. what does 1.01 represent in this expression?
Answers: 1
You know the right answer?
Let V be a vector space with subspaces Uand W. The set U∪W is the set of all vectors thatare in U or...
Questions


English, 21.04.2020 01:40

History, 21.04.2020 01:40






Mathematics, 21.04.2020 01:40





History, 21.04.2020 01:41

English, 21.04.2020 01:41

Spanish, 21.04.2020 01:41

History, 21.04.2020 01:41