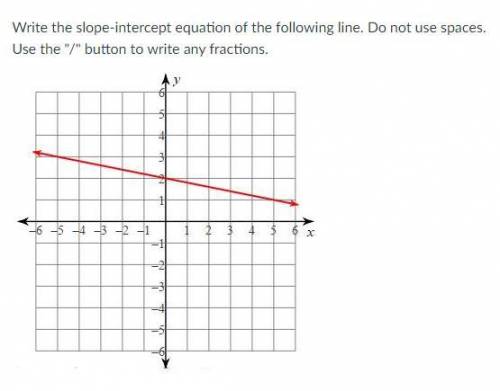
PLEASE HElp with math ... please and thank you
...

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 19:40
Afactory makes propeller drive shafts for ships. a quality assurance engineer at the factory needs to estimate the true mean length of the shafts. she randomly selects four drive shafts made at the factory, measures their lengths, and finds their sample mean to be 1000 mm. the lengths are known to follow a normal distribution whose standard deviation is 2 mm. calculate a 95% confidence interval for the true mean length of the shafts. input your answers for the margin of error, lower bound, and upper bound.
Answers: 3

Mathematics, 21.06.2019 20:10
The population of a small rural town in the year 2006 was 2,459. the population can be modeled by the function below, where f(x residents and t is the number of years elapsed since 2006. f(t) = 2,459(0.92)
Answers: 1

Mathematics, 22.06.2019 04:00
Dange measures and finds that she can do a vertical jump that is 27.5% of her height if dange is 48 inches tall how high can she jump
Answers: 3

Mathematics, 22.06.2019 04:20
When booking personal travel by air, one is always interested in actually arriving at one’s final destination even if that arrival is a bit late. the key variables we can typically try to control are the number of flight connections we have to make in route, and the amount of layover time we allow in those airports whenever we must make a connection. the key variables we have less control over are whether any particular flight will arrive at its destination late and, if late, how many minutes late it will be. for this assignment, the following necessarily-simplified assumptions describe our system of interest: the number of connections in route is a random variable with a poisson distribution, with an expected value of 1. the number of minutes of layover time allowed for each connection is based on a random variable with a poisson distribution (expected value 2) such that the allowed layover time is 15*(x+1). the probability that any particular flight segment will arrive late is a binomial distribution, with the probability of being late of 50%. if a flight arrives late, the number of minutes it is late is based on a random variable with an exponential distribution (lamda = .45) such that the minutes late (always rounded up to 10-minute values) is 10*(x+1). what is the probability of arriving at one’s final destination without having missed a connection? use excel.
Answers: 3
You know the right answer?
Questions

English, 18.08.2019 12:50

Mathematics, 18.08.2019 12:50

Mathematics, 18.08.2019 12:50

Physics, 18.08.2019 12:50

Mathematics, 18.08.2019 12:50

Mathematics, 18.08.2019 12:50




Chemistry, 18.08.2019 12:50

English, 18.08.2019 12:50

History, 18.08.2019 12:50

History, 18.08.2019 12:50


Mathematics, 18.08.2019 12:50


Mathematics, 18.08.2019 12:50



History, 18.08.2019 12:50