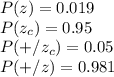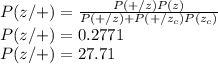Mathematics, 18.06.2021 03:20 davishernandez357
A pregnant woman lives in an area where the Zika virus is fairly rare---
1 in 1000 people have it. Still, she’s concerned, so she gets tested. There is a good but not perfect test for the virus---it gives a positive reading with probability .99 if the person has the virus and a positive reading with probability .05 if the person does not. Her reading is positive. How concerned should she be now? Probability---example We can use Bayes’ Theorem to calculate the probability she actually has the virus conditional on her positive test.
P(Z) = .001 (unconditional probability of having Zika)
P(Zc ) = .999 P(+|Z) = .99
P(+|Zc ) = .05
P(Z|+) = P(+|Z)P(Z)/{P(+|Z)P(Z) + P(+|Zc )P(Zc )} = .019
---less than 2% probability!!
The unconditional (prior) probability of her having the virus was quite low, 1/1000. We updated the probability based on the results of an imperfect test, but since it’s much more likely that the test was wrong (50 out of 1000 people without the virus test positive), our probability gets updated based on the positive test, but it doesn’t get updated that much. It goes from .0001 to .019.
Consider the example you saw in the lecture involving the Zika virus. We will start with the same set-up: A woman lives in a country where only 1 out of 1000 people has the virus. There is a test available that is positive 5% of the time when the patient does not have it, negative 1% of the time when the patient does have it, and otherwise correct. Recall that we computed that the woman’s chance of having the virus, conditional on a positive test, is less than 1.9%. (By the way, in Bayesian parlance, we call the initial, unconditional, probability the "prior" and the resulting conditional probability, after updating based on observations, the "posterior.")
6. Let the conditional probability we computed (1.9%) serve the role as the new prior. Compute the new probability that she has the virus (new posterior) based on her getting a second positive test.
7. How many positive test results would she have to receive in order to be at least 95% sure that she has the virus?
How many positive test results would she have to receive in order to be at least 95% sure that she has the virus?
Two
Three
Four
Five
Not possible to infer from the available information
In Question 6 we computed the probability of having the Zika virus after a second positive test by using the probability of having the Zika virus given a positive test (1.9%). Another way to compute this probability would be to use the fact that the two tests are independent and directly apply Bayes rule to derive the same result without using the technique employed in Question 6.
True or False: We would obtain the same probability using either method.
True
False
Not possible to infer from the available information

Answers: 1
Another question on Mathematics


Mathematics, 21.06.2019 19:40
Which is the solution to the inequality? 2 3/52 1/15 b< 3 2/15 b> 3 2/15
Answers: 1

Mathematics, 21.06.2019 20:30
In priyas math class there are 10 boys and 15 girls. what is the ratio of boys to girls in priyas math class? express your answer as a decimal
Answers: 1

Mathematics, 22.06.2019 00:50
F. a fair coin is thrown in the air four times. if the coin lands with the head up on the first three tosses, what is the probability that the coin will land with the head up on the fourth toss? a. 0 b. 1/16 c. 1/8 d. 1/2
Answers: 2
You know the right answer?
A pregnant woman lives in an area where the Zika virus is fairly rare---
1 in 1000 people have it....
Questions

Mathematics, 19.07.2019 03:10

Mathematics, 19.07.2019 03:10

Computers and Technology, 19.07.2019 03:10

Computers and Technology, 19.07.2019 03:10

Computers and Technology, 19.07.2019 03:10

Medicine, 19.07.2019 03:10



Computers and Technology, 19.07.2019 03:10

Computers and Technology, 19.07.2019 03:10



Engineering, 19.07.2019 03:10


Computers and Technology, 19.07.2019 03:10

Computers and Technology, 19.07.2019 03:10

Mathematics, 19.07.2019 03:10