
Mathematics, 24.09.2021 14:10 kleathers97
Given that 'n' is any natural numbers greater than or equal 2. Prove the following Inequality with Mathematical Induction
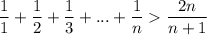
Show your work too — thanks!

Answers: 1
Another question on Mathematics


Mathematics, 21.06.2019 19:50
The graph shows the distance kerri drives on a trip. what is kerri's speed?
Answers: 3

Mathematics, 21.06.2019 20:00
Someone answer asap for ! the following statements are true about the coins calvin and sasha have collected. * calvin and sasha has the same amount of money. * calvin has only quarters. * sasha has dimes, nickels, and pennies * calvin has the same number of quarters as sasha has dimes. * sasha has $1.95 in coins that are not dimes. exactly how many quarters does calvin have?
Answers: 3

Mathematics, 21.06.2019 22:30
For the chance to be team captain, the numbers 1-30 are put in a hat and you get two chances to pick a number, without replacement. which formula correctly shows how to find the probability that you choose the number 1 and then 2?
Answers: 1
You know the right answer?
Given that 'n' is any natural numbers greater than or equal 2. Prove the following Inequality with M...
Questions

Social Studies, 12.12.2020 16:40




Mathematics, 12.12.2020 16:40


Mathematics, 12.12.2020 16:40

Mathematics, 12.12.2020 16:40


Mathematics, 12.12.2020 16:40






Chemistry, 12.12.2020 16:40

Mathematics, 12.12.2020 16:40

Biology, 12.12.2020 16:40


Mathematics, 12.12.2020 16:40



