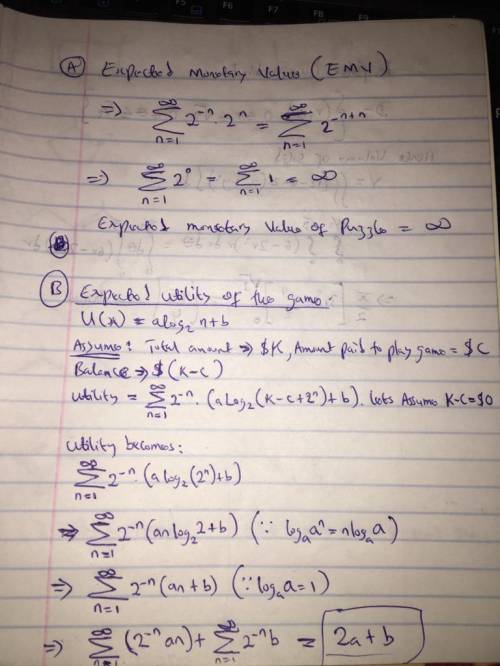The St. Petersburg paradox goes as follows. A fair coin is tossed repeatedly until it comes up heads. If the first heads appears on the nth toss, you win $2 n . First, show that the expected monetary value of this game is infinite (the paradox is that no one would actually pay a huge amount to play this game). Second, consider a possible resolution of the paradox: suppose your utility for money is given by a log 2 x b where x is the number of dollars you have. Suppose you start with 0 dollars, what is the expected utility of this game

The accompanying table shows the numbers of male and female students in a particular country who received bachelor's degrees in business in a recent year. complete parts (a) and (b) below. business degrees nonbusiness degrees total male 189131 634650 823781 female 169539 885329 1054868 total 358670 1519979 1878649 (a) find the probability that a randomly selected student is male, given that the student received a business degree. the probability that a randomly selected student is male, given that the student received a business degree, is nothing. (round to three decimal places as needed.) (b) find the probability that a randomly selected student received a business degree, given that the student is female. the probability that a randomly selected student received a business degree, given that the student is female, is nothing. (round to three decimal places as needed.)

Acd that is originally priced at $15.85 red-tagged for the sale. what is the sale price of the cd

What is the location of point g, which partitions the directed line segment from d to f into a 5: 4 ratio? –1 0 2 3